Understanding the surface area of a sphere is essential in various fields of science, engineering, and everyday life applications. Whether you’re a student grappling with geometry or a professional looking to apply these principles practically, this article provides a comprehensive guide to understanding and calculating the surface area of a sphere.

Key Takeaways

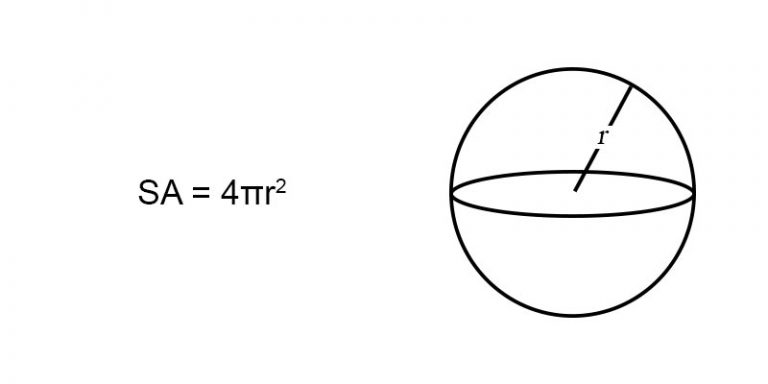
• The surface area of a sphere is calculated using the formula: 4πr².
• Understanding the surface area is crucial for fields such as physics, engineering, and architecture.
• Practical applications range from designing spherical objects to calculating material requirements.

What is a Sphere?

A sphere is a perfectly round three-dimensional shape, similar to a ball. Every point on the surface of a sphere is equidistant from its center. This distance is known as the radius (r). The sphere is a fundamental shape in geometry and is widely studied for its unique properties and applications.

Understanding the Surface Area

The surface area of a sphere refers to the total area that the surface of the sphere occupies. It is an important concept in geometry and is crucial for determining how much material is needed to cover a spherical object, among other applications.

Calculating the Surface Area of a Sphere

The formula for calculating the surface area of a sphere is:

Surface Area = 4πr²

Where π (pi) is a constant approximately equal to 3.14159, and r is the radius of the sphere. This formula is derived from the integration of the sphere’s circular cross-sections.

Derivation of the Formula

To derive the formula for the surface area of a sphere, consider the sphere as a series of infinitesimally thin circular disks stacked upon each other. By integrating the circumferences of these disks from the top to the bottom of the sphere, we arrive at the formula 4πr².

Practical Applications

Understanding the surface area of a sphere has numerous practical applications:

• Engineering: In designing spherical tanks or domes, engineers need to calculate the surface area to determine the amount of material required.
• Physics: The surface area is critical in understanding phenomena such as radiation and heat transfer, where the sphere often serves as a model for celestial bodies or atoms.
• Architecture: Architects may use spherical designs in structures, necessitating accurate surface area calculations for construction purposes.
• Everyday Life: From sports equipment like balls to decorative items, understanding the surface area helps in manufacturing and cost estimation.

Examples and Problem Solving

Example 1: Calculating the Surface Area of a Basketball

Consider a standard basketball with a radius of 12 cm. To find its surface area:

Surface Area = 4π(12 cm)² = 4π(144 cm²) = 576π cm² ≈ 1808.64  cm²

Thus, the surface area of the basketball is approximately 1808.64 square centimeters.

Example 2: Designing a Spherical Water Tank

Imagine designing a spherical water tank with a radius of 5 meters. The surface area calculation is crucial for determining the amount of paint needed for coating:

Surface Area = 4π(5 m)² = 4π(25 m²) = 100π m² ≈ 314.16 m²

The surface area of the tank is approximately 314.16 square meters.

Common Mistakes to Avoid

When calculating the surface area of a sphere, it’s essential to avoid common pitfalls:

• Incorrect Radius: Ensure that the radius is accurately measured and used in the formula.
• Ignoring Units: Always include and convert units appropriately to maintain consistency.
• Rounding Errors: Use a sufficient number of decimal places for π to ensure accuracy.

The surface area of a sphere is a fundamental concept in geometry with wide-ranging applications in science, engineering, and everyday life. By mastering the formula 4πr² and understanding its derivation and applications, you can tackle a variety of practical problems with confidence. Whether you’re calculating the material for a spherical dome or understanding the physics of celestial bodies, the surface area of a sphere is a crucial tool in your mathematical toolkit.

By grasping these concepts, you’re well-equipped to apply this knowledge in both academic and practical settings, ensuring precision and efficiency in your calculations and designs.